Strongly monotone
In functional analysis, an operator 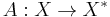 where X is a real Hilbert space is said to be strongly monotone if
where X is a real Hilbert space is said to be strongly monotone if
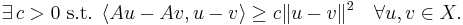
This is analogous to the notion of strictly increasing for scalar-valued functions of one scalar argument.
See also
References
- Zeidler. Applied Functional Analysis (AMS 108) p. 173
‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›
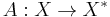 where X is a real Hilbert space is said to be strongly monotone if
where X is a real Hilbert space is said to be strongly monotone if